最优化理论算法：模拟退火算法寻找函数最值Matlab实现

问题

最优化理论与算法课程作业题，用遗传算法求解如下问题：

$$max \quad f(x) = x \cdot sin(3x) , -1 \le x \le 30$$

算法思路

退火算法具体思路可以理解为晚上喝醉后爬山，目标是到山顶。由于是晚上，所以这个人只能看见附近一定距离的山的情况。刚开始是醉的，所以这个人迷迷糊糊随机爬，可能按正确的方向向上爬，也可能向下爬，但是随着醉酒程度慢慢减轻，这个人慢慢看清了附近的形势，于是向上爬。最后达到山顶。

而模拟退火算法来源于固体退火原理，是一种基于概率的算法，将固体加温至充分高，再让其徐徐冷却，温度高时，固体内部粒子无序，内能大，而徐徐冷却时粒子渐趋有序，在每个温度都达到平衡态，最后在常温时达到基态，内能减为最小。

冷却初期的高温对应了醉酒爬山初期醉酒情况，这时候无序，按一定的概率接受向下的方向。后期温度降低对应酒醒，这时候接受错误方向的概率非常低。

退火算法的好处是按照一定概率接受错误方向，可以跳出局部最优解，并且随着进度慢慢降低接受错误方向的概率。

流程图直接放一张PPT的流程图：

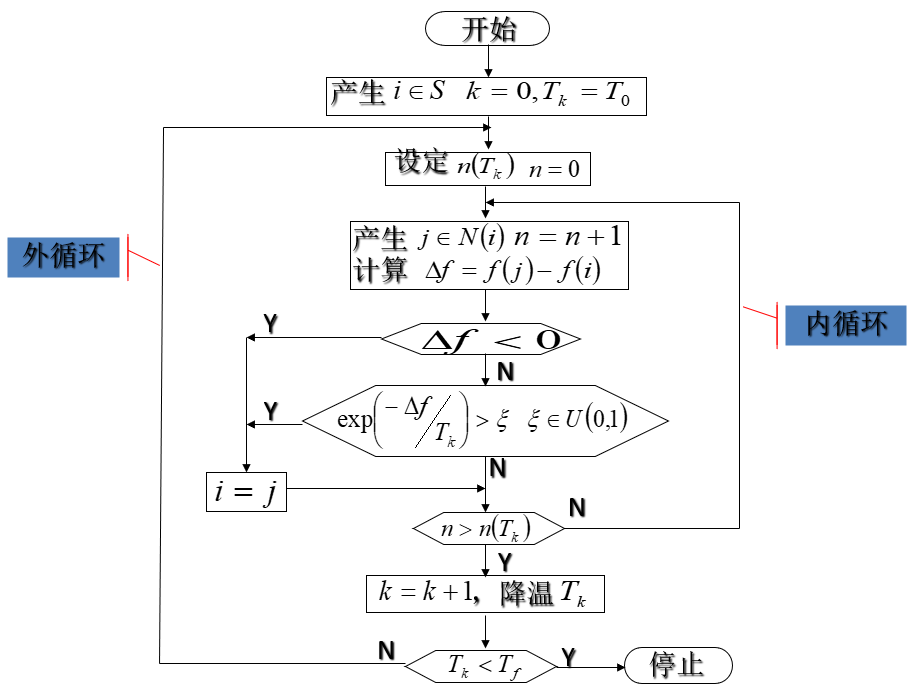
初始化

选取区间任意解，设定足够高的初始温度。

产生领域解

在初始解（上一解）附近随机产生一个领域解，即随机找一个方向爬山。

领域解接受判断

如果领域解的方向是正确方向（此题即函数值更大），则接受领域解。如果是错误方向，则按照一定概率接受，接收概率与当前温度相关。

判断

若内循环次数大于预设次数，认为这个温度下爬山已经爬够了，降温。否则继续爬。

降温

按照比例或者增量降温，如果温度达到低温条件，则停止。否则降温后继续爬山。

Matlab实现

clear;
clc;
close all;

% 目标函数
func = @(x) x * sin(3 * x);

x0 = 10; 		% 初始解
T0 = 1e4; 		% 初始温度
Tf = 1e-4; 		% 终止温度
r = 0.97; 		% 降温指数
epochs = 1e3;	% 迭代次数
Tk = T0;
xk = x0;

while true
    for i = 1:epochs
        x_new = xk + rand(1);
        if x_new > 30
            x_new = 30 - rand(1);
        end
        if x_new < -1
            x_new = -1 + rand(1);
        end
        delta_f = func(x_new) - func(xk);
        if delta_f > 0
            xk = x_new;
        else
            esp = rand();
            if exp(delta_f ./ Tk) > esp
                xk = x_new;
            end
        end
    end
    Tk = Tk * r;
    if Tk < Tf
        best_x = xk;
        best_f = func(xk);
        break;
    end
end

结果

最优解 x = 29.849416， 目标函数值 f = 29.846949