问题
最优化理论与算法课程上留了一道作业题,用启发式搜索算法求解数独问题。数独如下。

算法思路
基础算法上采用深度优先搜索,即找到一个空位就填入一个符合数独要求的数字,即候选数,然后扩展该节点,继续找下一个空位填入一个候选数,扩展节点。如果发现有空位没有候选数可以填,就回溯。直到所有的空位都填满数字。
在此基础上,考虑启发式搜索,即寻找空位时候,先求出所有空位的候选数的数量,然后找到候选数数量最少的空位作为扩展的节点。可以减少搜索次数。
算法流程图如下:

Matlab实现
用matlab实现该算法,其中结构体数组poplist为open表储存了扩展的节点。candidate为当前节点情况下的最少候选数空位的候选数,index为节点索引。
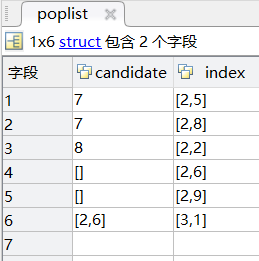
代码结构:
主函数:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
| clear;
clc;
close all;
% 数独矩阵
board = [
0 0 0 7 0 2 0 0 0;
1 0 0 0 4 0 0 0 7;
6 5 0 0 0 0 0 9 4;
4 7 0 8 0 1 0 6 2;
0 0 0 0 0 0 0 0 0;
5 8 0 2 0 9 0 1 3;
8 6 0 0 0 0 0 7 5;
9 0 0 0 6 0 0 0 8;
0 0 0 9 0 8 0 0 0;
];
% 主函数
poplist = struct(); % 储存待扩展节点的open表
i = 1; % poplist迭代索引
isok = false; % 结束flag
epoch = 1; % 迭代变量
[poplist(i).candidate, poplist(i).index, isok] = cal_candidate(board);
while true
if isok
disp(epoch);
break;
else
% 判断poplist最后一个节点是否为空
if isempty(poplist(end).candidate)
% 该位置的候选数空,说明坏节点,还原为该位置为0,回溯
index = poplist(end).index;
board(index(1), index(2)) = 0;
poplist(end) = [];
i = i - 1;
else
% 该位置候选数不为空,赋值,更新poplist,扩展节点
index = poplist(end).index;
board(index(1), index(2)) = poplist(end).candidate(1);
poplist(end).candidate(1) = [];
i = i + 1;
[poplist(i).candidate, poplist(i).index, isok] = cal_candidate(board);
end
end
epoch = epoch + 1;
end
|
候选数计算函数:cal_candidate()
函数统计所有空位候选数的函数,返回候选数最少的空位坐标及其候选数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| % 函数:计算所有0处的候选数,并返回最少候选数的空位坐标及候选数list
function [cand_list, cand_index, isok] = cal_candidate(board)
k = 1;
candidate = struct();
empty = false; % board是否还有空位flag,默认没有空位
for i = 1:9
for j = 1:9
if board(i, j) == 0
empty = true; % 能找到0, 说明board还有空位
candidate(k).list = find_candidate(board, i, j);
candidate(k).length = length(candidate(k).list);
candidate(k).index = [i, j];
k = k + 1;
end
end
end
if empty
% 将空位按照候选数数量升序
[~, index] = sort([candidate.length]);
candidate = candidate(index);
cand_list = candidate.list;
cand_index = candidate.index;
isok = false;
else
cand_list = [];
cand_index = [];
isok = true;
end
end
|
寻找候选数函数:find_candidate()
寻找当前空位所有的候选数list
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| % 寻找当前位置候选数list
function list = find_candidate(board, x, y)
numbers = [1 2 3 4 5 6 7 8 9];
for i = 1:9
% 扫描行
if board(x, i) ~= 0
numbers(numbers == board(x, i)) = [];
% 如果发现非0数,则将numbers中该数删除
end
% 扫描列
if board(i, y) ~= 0
numbers(numbers == board(i, y)) = [];
% 如果发现非0数,则将numbers中该数删除
end
end
% 扫描九宫格
start_i = ceil(x / 3) - 1;
start_j = ceil(y / 3) - 1;
for i = 1:3
for j = 1:3
if board(i + start_i * 3, j + start_j * 3) ~= 0
numbers(numbers == board(i + start_i * 3, j + start_j * 3)) = [];
% 如果发现非0数,则将numbers中该数删除
end
end
end
list = numbers;
end
|
结果
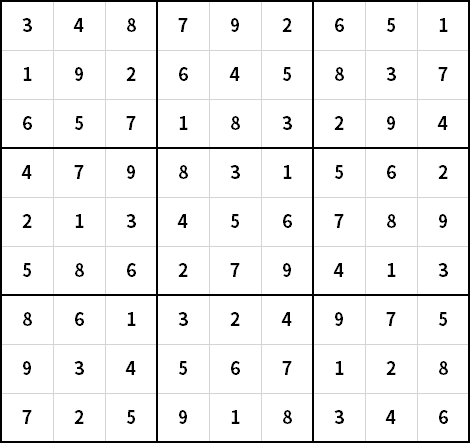
作业中数独问题比较简单,迭代52次,不需要回溯,结果如下:
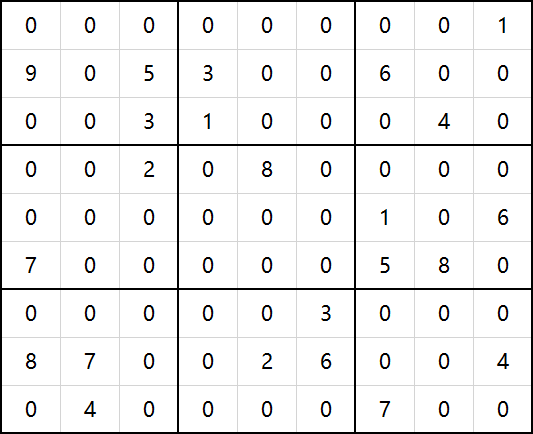
后测试了难度更大的数独问题。
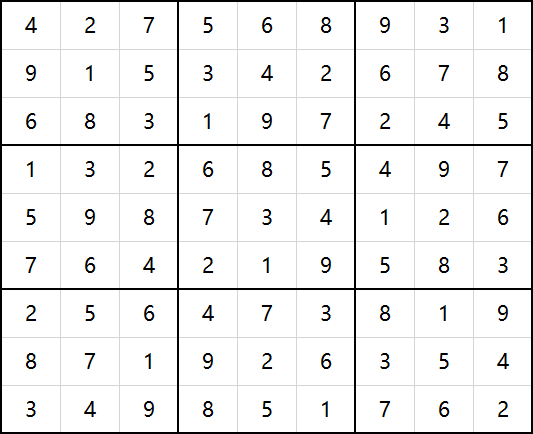
共迭代1439次,结果如下:
参考
- 启发式搜索算法求解数独




